Study Objectives

• To define activity, activity coefficient, concentration, diffusion, flux, molality, molarity, normality, osmolality, osmosis, pressure and radioactivity.
• To describe the diffusion potential, the equilibrium potential, facilitated diffusion, the Donnan-effect, the resting membrane potential, the action potential, and membrane transport including that of glucose.
• To calculate the equilibrium potential, osmotic pressure and other variables from relevant variables given.
• To draw the action potential curve.
• To explain the colloid osmotic pressure of plasma, hyponatraemia, overbreathing, radioactive decay and the elimination rate constant, the nerve conduction, signal transduction, the function of the action potential, the Na⁺-K⁺ -pump and the transport proteins.
• To use the ideal gas law and the above concepts in problem solving and case histories.

Principles

• The ideal gas law relates the pressure P, the volume V, and the number of mol of the gas n, to the Kelvin temperature T: P* V = n*R*T.

• At standard temperature, pressure, dry (STPD) the volume occupied by 1 mol of any ideal gas is 22.4 litre (l). - By analogy in an ideal solution, one mol of solute will exert an osmotic pressure of one atmosphere, if it is dissolved in 22.4 l of water. Van´t Hoff´s law for ideal solutions is an equivalent to the ideal gas law.

Definitions

Absolute Temperature (T) is measured in Kelvin or K from the absolute zero point (-273 ^oC).

Activity is a corrected concentration measure of any species (ie, the free concentration multiplied by the activity coefficient). The activity is often measured with ion selective electrodes. - In diluted solutions - below 10^-3 molar - there is no correction for uncharged molecules.

Activity coefficient is the fraction of the free ions, which is chemically active. - For sodium the activity coefficient is 0.75 in many biological solutions.

Action Potential (AP) is an all-or-none electrical signal, which appears as a positive wave when recording internally. The AP is conducted with the same shape and size along the whole length of a muscle cell or a nerve fibre.

Amphipathic molecules contain both a polar and a non-polar region.

The membrane potential difference is defined as the potential inside the cell minus the potential outside the cell – the difference is transiently reversed during an AP.

Becquerel (1 Bq) is the preferred unit for disintegration rate of radioactive decay, namely one radioactive disintegration per s. Disintegration rates were previously expressed in Curies (Ci), in honour of Marie Curie, who discovered radium.

Concentration (C or brackets around a substance [Na⁺]) is the mass or moles (mol) per unit of fluid volume.

Diffusion is a net transport of atoms or molecules caused by their random thermal motion in an attempt to equalise concentration differences (DC).

The Donnan effect is the extra osmotic pressure of protein solutions caused by impermeable protein molecules resulting in uneven distribution of small, permeant cations and anions (in blood plasma).

The elimination rate constant (k) is the fraction of the total amount of a given substance in the distribution volume of the body eliminated per time unit. Elimination with a constant rate is exponential. The half-life for a substance eliminated exponentially is equal to 0.693 k^-1. This is just a simple mathematical deduction.

Flux (J) is the amount of a substance transported along a pressure gradient through an area unit (A is measured in m²) of a membrane in moles per second (s). Convective flux is the net amount of molecules transported through A per time unit (mol s^-1 m^-2), caused by a pressure gradient and fluid (liquid or air) volume transport.

An ideal semipermeable membrane is permeable to water only, but impermeable to all solutes. Most real semipermeable membranes are permeable to water and to low molecular substances (crystalloids), but not to macromolecular substances (colloids such as proteins).

Molar concentration (molarity) is the number of moles of a substance totally dissolved per litre (l) of solution - often given in mmol per l or mM. One mol of a substance is the amount of that substance containing Avogadros number, 6.022 *10²³ molecules per mol.

Molality is the number of mol totally dissolved substance per kg of solvent, frequently water. One equivalent is the molar mass of all the ions that contain 6.022 *10²³ single charges or valences when fully dissociated.

Motility is the reciprocal resistance of a molecule towards movements.

Normality of a solution is the number of equivalents per l (Eq l^-1).

Osmolality is a measure of the osmotic active particles in one kg of water. Plasma-osmolality is given in Osmol per kg of water. Water occupies 93% of plasma in healthy persons.

Osmolarity is the number of osmotically active particles dissolved in a litre of solution.

A permeable membrane allows the passage of all dissolved substances and the solvent (mainly water).

A selectively permeable membrane is permeable to a particular compound (sucrose, Na⁺, Ca²⁺, anions only or to cations only).

• Pressure (P) is measured as force per area unit - that is in Newton per square m or Pascal.
• Osmosis is transport of solvent molecules (mainly water) through a semipermeable membrane. Osmotic pressure (p) is the hydrostatic pressure, that must be applied to the side of a rigid ideal semipermeable membrane with higher solute concentration in order to stop the water flux, so that the net water flux is zero.
• Radioactivity. Some nuclei are unstable or radioactive, because they release certain particles such as helium nuclei or electrons. Other radioactive substances emmanate gamma-rays with an extremely short wavelength. All radioactive decay processes follow an exponential pattern. If N_o is the initial number of unstable nuclei, the number of nuclei remaining after a time t (N) is given by N = N_o * e^-kt, where k is a constant characteristic of each nuclide, called the disintegration constant. This is the law of radioactive decay (Eq. 1-6).
• Volume (V) in litres (l). Standard temperature, pressure, dry (STPD) is an abbreviation for a volume at standard temperature of 273 K, standard pressure of 101.3 kPa or 760 mmHg, and dry air.

Essentials

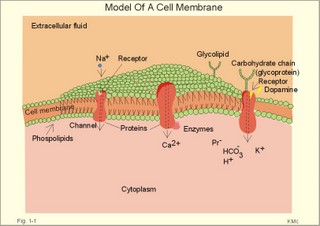
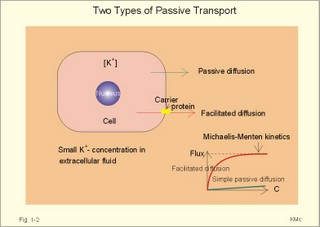
Three topics are treated here:

1. Transport through membranes,2. Resting membrane potentials, and 3. Action potentials.

1. Transport through membranes

Membrane transport refers to solute and solvent transfer across both cell membranes, epithelial and capillary membranes.

1a. Membranes

Biological membranes are composed of phospholipids stabilised by hydrophobic interactions into bilayers (Fig. 1-1). The membranes contain approximately 50% lipids and 50% proteins.

click on the image to see a larger view in a new window.

Fig. 1-1: Model of a cell membrane built by phospholipids separating receptors, channels, proteins (Pr^-), glycoproteins (receptors, antigens etc) and glycolipids.

Phospholipids are amphipathic. One region is polar consisting of charged choline, etanolamine and phosphate head-groups (bullets in Fig. 1-1). The other region is non-polar, consisting of tails of fatty acyl chains (Fig. 1-1). The non-polar regions tend to avoid contact with water by self-association. Any other arrangement with disruption of hydrogen bonds (between O and H atoms) of water has a high energy cost. Integral proteins are deeply imbedded in the membrane, and the model shows 3 protein molecules spanning the membrane (ie, transmembrane proteins). Surface proteins are not shown. The proteins carry receptors to which transmitter substance bind. Carbohydrate chains are shown forming glycolipids with antigenic or receptor function, or glycoproteins with other receptor functions.

The molar concentration (molarity) is the number of mol totally dissolved substance per litre (l) of solution - often given in mmol per l or mM. Ions in plasma are conventionally measured in mM with flame-photometry by the ability to absorb monochromatic light. Na⁺ is mainly dissolved in the water phase of plasma (93%). The [Na⁺] in plasma is therefore smaller than the Na⁺-activity which is recorded in the water phase alone with ion selective electrodes. For conventional reasons ion selective electrodes are calibrated to match the well-known flame photometry values, although the activity is the biological important variable. Molality, normality, and flux are described above in Definitions.

Mechanical, electrical, thermal, or gravitational forces drive migration of molecules. These forces move the molecules passively in a direction determined by the vector of the force.

Diffusive flux (J^dif) is the movement of molecules by diffusion caused by a concentration gradient (dC/dx) in the direction x. The diffusion coefficient (D) is a proportionality constant that relates flux to the concentration gradient (dC/dx). Einstein defined D as (k×T×B), where T is absolute temperature and B is motility of molecules. Motility is the reciprocal resistance towards movements (velocity/N or m*s^-1*N^-1). The concept (k*T) is the thermal, molecular energy. A molecule diffuses from higher to lower concentration that is down its concentration gradient. Accordingly, dC/dx has a negative slope, when molecules diffuse in the direction x. Then, it is easy to calculate the diffusive flux (per m²) according to Eq. 1-2. This relationship was first recognized as early as in 1855 by the anatomist and physiologist Fick, and it has since been named after him: Fick's first law of diffusion. The flux by simple passive diffusion is directly proportional to the concentration of dissolved molecules (Fig. 1-2).

Fig. 1-2: Two types of passive molecular transport: Simple diffusion and the much larger facilitated diffusion. C is concentration.

Einstein's relation states that for average molecules in biological media, the mean displacement squared, (dx)², is equal to 2 multiplied by D and by the time (t) elapsed, since the molecules started to diffuse (see Eq. 1-3). For molecules with D = 10^-9 m² s^-1, the time required to diffuse 1 mm is 0.5 milli-second (ms). To diffuse 10 and 100 mm, the time required increases 100-fold each time: 50 ms and 5000 ms.

Facilitated diffusion takes place through transport proteins not linked directly to metabolic energy processes (Fig. 1-2). Facilitated diffusion shows saturation or Michaelis-Menten kinetics, because the number of transport proteins is limited. The saturation kinetics is different from the energy limitation in primary active transport. Amino acids, glucose, galactose and other monosaccharides cross many cell membranes by facilitated diffusion.

An ideal semipermeable membrane is permeable to water only, but impermeable to all solutes. Most real semipermeable membranes are permeable to water and to low molecular substances (crystalloids), but not to macromolecular substances (colloids such as proteins).

An ideal ion-selective membrane is permeable to anions only or to cations only (Na⁺, Ca²⁺, or to Cl^- and NO₃^-). Ion-selective membranes are used in ion-selective electrodes to measure the activity of selective ions in plasma water (Table 1-1).

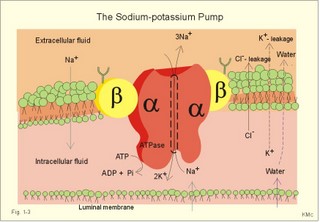
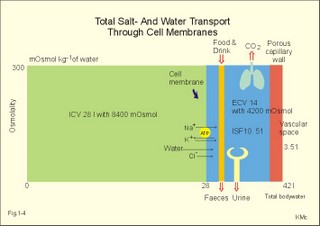
The relation between the potential difference measured with an ion-selective electrode and the activity (ionised or fully dissociated form) for a certain ion (eg, K⁺) is given by the Nernst equation (Eq. 1-5).

Osmosis is transport of solvent molecules (mainly water) through a semipermeable membrane. The water flows from a compartment of high water concentration (or low solute concentration) to one of low water concentration (or high solute concentration). The greater difference between the solute concentration of the two compartments, the more is water unevenly distributed between the two compartments. Water diffuses down its chemical potential gradient into the compartment with higher solute concentration, causing the chemical potential gradient to be reduced until solute equilibrium is reached.

Osmotic pressure is the hydrostatic pressure, that must be applied to the side of an ideal semipermeable membrane with higher solute concentration in order to stop the water flux, so that the net water flux is zero.

The colligative properties of water are strictly related to the solvent or water concentration alone. Water molecules are bound together by hydrogen bonds in clusters of several hundred molecules, forming a structure looking almost like crystals. Sites between the clusters, where the distance between water molecules are larger than elsewhere are called bubble nuclei because these sites seem to initiate formation of gas bubbles in decompression sickness. These sites are also likely locations for substances dissolved in water. With decreasing water concentration, the water vapour tension, and the freezing point is reduced, whereas the boiling point, and the osmotic pressure of the solution is increased as compared with pure water. The size of the osmotic pressure of a solution depends of the number of dissolved particles per volume unit.

The osmotic pressure (p) depends on the absolute temperature (T Kelvin or K) and on the number of dissolved particles per volume unit (N/V equal to the molar fraction).

This relationship was first recognized by van't Hoff and applies to ideal solutions only. Real physiological solutions, such as the cytosolic phase and extracellular fluid, differ from the ideal solutions, which are very dilute.

A correction factor called the osmotic coefficient (f) corrects for these differences in osmolality. For physiologic electrolytes it is 0.92 - 0.96, and for carbohydrates it is 1.01.

A solution has the ideal osmolarity one, when it contains (6.022* 10²³) osmotically active particles per l. Diluted solutions have an osmolar concentration or osmolarity (Osmol per l) numerically equal to the sum total molarity of all dissolved particles (mol per l). In biological solutions the molarity is different from osmolar concentration. The number of Osmol per l is: (f N/V). - The corrected van't Hoff law is developed in Eq. 1-4.

Osmolality is simply the number of mol per kg of water in the fluid frequently given as mOsmol kg^-1. Fully dissociated molecules have twice the osmolality of undissociated molecules. Plasma- osmolality can be approximated by the calculation expressed in Eq. 1-7. Plasma-osmolality is measured by freeze point depression or by boiling point increase. The osmolality of the ICV is approximately 290 mOsmol kg^-1, which is simplified to 300 mOsmol kg^-1 in Fig. 1-4. The osmolality of the extracellular fluid must be the same, since cell membranes are not rigid, so they cannot carry any essential pressure gradient. The total number of mOsmol in the ICV and ECV of a standard person is thus 8400 and 4200, respectively (Fig. 1-4).

The colloid osmotic pressure is equal in magnitude to the hydrostatic pressure, which must be applied at the luminal side of the capillary barrier, in order to stop net transport of water caused by uncharged colloids in the blood plasma. Colloids are mainly plasma proteins.

The osmotic pressure is equal in magnitude of a certain hydrostatic pressure. This pressure column must be applied to the solution to restore the free energy or chemical potential of its water to that of pure water. The tendency of water to pass a membrane depends on its chemical potential (ie, vapour pressure). The chemical potential of water decreases with solutes present and with decreasing temperature.

Uniformly distributed substances in diluted solutions behave like gas molecules at atmospheric pressure (atm). The osmotic pressure can be expressed as P_osmot = C × RT, which is the equivalent of the ideal gas equation (P × V = nRT). Here C is the concentration of dissolved solutes, and the derivation of the relationship is based on the chemical potential of water. R is the gas constant (= 0.082 l × atm × Osmol^-1 × K^-1). At standard temperature, pressure, dry (STPD) the volume occupied by 1 mol of any ideal gas is 22.4 l. Thus, STPD is an abbreviation for a volume at standard temperature of 273 K, standard pressure of 101.3 kPa or 760 mmHg, and dry air. In an ideal solution, one mol of solute will by analogy be dissolved in 22.4 l of water, and will exert an osmotic pressure of one atmosphere.

In biological solutions at 310 K, such as an ultrafiltrate of plasma (interstitial fluid, ISF), with an osmolality of 0.300 Osmol per kg water, the osmotic pressure must be:

Only net gradients across endothelial and plasma membranes are important, and they depend upon protein concentration gradients. This is because all the electrolytes (crystalloids) have diffused to equilibrium across the capillary endothelial membrane, whereas proteins (colloids) cannot.

The average colloid osmotic pressure (p_coll) of plasma is approximately 3.6 kPa (27 mmHg). The dissolved proteins have a molality of 1 mmol per kg water, and a net average of 17 negative charges per molecule (ie, 1 mmol kg^-1 or 17 mEq kg^-1). Milli-Equivalents abbreviates mEq. The proteins are directly responsible for 2.4 kPa (18 mmHg). The remaining 1.2 kPa (9 mmHg) of the colloid osmotic pressure is due to the unequal distribution of permeable ions, the Gibbs-Donnan law or the Donnan effect (see below).

1c. The Donnan effect across the capillary membrane

Let us consider a closed system with two compartments separated by a rigid membrane that is permeable to water and to small ions. In the presence of solutions with different NaCl concentrations, water and ions permeate rapidly in both directions across the membrane. Electrical neutrality in each of the two solutions requires that the simultaneous movement of Cl^- match any net movement of Na⁺, so the equivalents of anions and cations are the same. The number of times the two ions collide with one side of the membrane is proportional to the product of their concentrations: [Na⁺] × [Cl^-]. At equilibrium the fluxes of NaCl in each direction are identical, and ultimately the concentrations are the same all over.

Let us now add protein to one compartment (compartment_p modelling streaming plasma), which is separated by a membrane (modelling the capillary endothelial membrane) from the other compartment (compartment_ISF modelling interstitial or tissue fluid). The model still contains only Na⁺ and Cl^- that can cross the membrane. At equilibrium the product of concentrations of the two ions on either side of the membrane must be equal, and the transmembrane potential corresponds to the equilibrium potential of the small permeant ions (the Nernst equation, Eq 1- 5). Transforming the Nernst equation reveals that the concentration product of any pair of diffusible ions is identical on either side of the membrane at equilibrium:

[Na⁺]_ISF × [Cl^-]_ISF = [Na⁺]_p × [Cl^-]_p.

On the plasma side, which contains impermeant anions (negative proteinates), the concentration of permeant anion (Cl^- is the model) must always be less than on the interstitial fluid side. The concentration of permeant cation (Na⁺ is the model) must always be greater than in the ISF.

The sum of permeant anion and cation concentrations in plasma is always greater than the sum of the same anion and cation concentrations in ISF:

[Na⁺]_ISF = [Cl^-]_ISF ; [Na⁺]_p + [Cl^-]_p > [Na⁺]_ISF + [Cl^-]_ISF

This is a simple mathematical argument: The sum of unequal sides of a rectangle is greater than the sum of the sides of the square with the same area. It explains why the osmotic pressure in plasma exceeds that of the tissue fluid. This is not due to the plasma proteins alone, but is also due to the higher concentration of small, permeant ions in the plasma.

The Donnan effect is the extra osmotic pressure of protein solutions caused by the uneven distribution of small, permeable cations and anions. The Donnan effect causes a 5% and 10% concentration difference across the capillary barrier between the plasma and ultrafiltrate concentrations of monovalent and divalent ions, respectively.

In the above equations Na⁺ and Cl^- are model ions for all the cations and anions. In our body other anions and cations are present, the Na⁺ and Cl^- concentrations are not alike, and the capillary membrane is far from rigid. Nevertheless, the Donnan equilibrium implies an accumulation of charges on the side with the negatively charged proteins. This potential difference across the capillary membrane is termed the Donnan potential – a potential, which is developed across cell membranes without a sodium-potassium pump.

The Donnan factor at the capillary membrane is 0.95, so a plasma- [ Na^+] of 150 mmol measured in each kg of plasma-water is in equilibrium with 142 mM in the interstitial fluid between the cells.

Strictly speaking, there is no such thing as a cell with rigid cell walls in the animal kingdom, so the Donnan effect is theoretically unfounded in animal cell membranes – except at the capillary barrier.

1d. The Na⁺-K⁺-pump.

The Na⁺-K⁺-pump is a transmembrane protein in the cell membrane (Fig. 1-3). The pump contains a channel, which consists of two double subunits: 2 a - and 2 b - subunits. The catalytic subunit (a ) is an Na⁺-K⁺-activated ATPase of 112 000 Dalton, and the b -subunit is a glycoprotein of 35 000 D.

Fig. 1-3: The Na⁺-K⁺-pump consists of 2 a - and 2 b - subunits (Pi = Phosphate).

The pump is a primary active transporter, because it uses the cellular energy of the terminal phosphate bond of ATP (Fig. 1-3). The Na⁺-K⁺-pump transports 3 Na⁺ out of the cell and 2 K⁺ into the cell for each ATP hydrolysed. This is a net movement of positive ions out of the cell, and therefore called an electrogenic transport. The constant influx of Na⁺ is shown as well as the leakage of K⁺- and Cl^-. In a steady state the net transport of each ion across the resting membrane is zero.

The Na⁺-K⁺-pump is located in the basolateral exit-membrane of the epithelial cell (Fig. 1-3). The primary active ion-transport provides metabolic energy for the secondary water absorption through the luminal membrane. Hereby, the active pump in the exit-membrane drives the luminal transport across the entry membrane. This transport of NaCl and water is surprisingly nearly isotonic. The bulk flow can take place against a large osmotic gradient, and increases in diluted solutions. The entry membrane is often highly permeable to water.

The Na⁺-K⁺-pump builds up a high cellular electrochemical gradient for K⁺ and indirectly for Cl^- (Fig. 1-3). The water outflux is coupled to the outward transport of K⁺ and Cl^-. The interstitial fluid receives ions and glucose, causing its osmolarity to increase. The osmotic force causes water to enter the interstitial fluid via the cell membranes and the gaps between the cells (tight junctions). This in turn causes the hydrostatic pressure in the interstitial fluid to rise. The hydrostatic force transfers the bulk of water, ions and molecules through the thin-walled, tubular capillaries to the blood. When excess of water (solvent) passes through tight junctions, they lose part of their tightness and the solvent water drags many Na⁺/Cl^--ions out (solvent drag).

In a healthy standard person nutrients and oxygen are transported into the cell interior from the extracellular fluid through the cell membrane (Fig. 1-4). The intracellular fluid volume, ICV, is 26-28 l. The extracellular fluid volume (ie, ECV of 14 l) consists of the circulating blood plasma (3-3.5 l) and the interstitial fluid (ISF) with a volume of 10.5-11 l in the spaces between cells. Total body water (here 42 l) accounts for 60% of body weight. The body is cleared of 24 mol of carbon dioxide by the lungs in 24 hours and of other substances by the kidneys (Fig. 1-4). A yellow tube on the diagram symbolises the gastrointestinal channel, where nutrient molecules are absorbed and waste products are eliminated through the liver bile.

Fig. 1-4: Salt- and water- transport through a cell membrane separating the intracellular and extracellular compartment.

The diagram also shows the Na⁺-K⁺-pump together with leakage of K⁺, Cl- and water (Fig. 1-4). The net transport of each substance is zero in the steady state.

The Na⁺-K⁺-pump is responsible for maintaining the high intracellular [K⁺] and the low intracellular [Na⁺]. The energy of the terminal phosphate bond of ATP is used to actively extrude Na⁺ and pump K⁺ into the cell.

Jens Christian Skou of Denmark initiated the study of the Na⁺-K⁺-pump already in the 1950ties and received the Nobel Prize for his contribution to basic chemistry and physiology in 1997.

The membrane also contains many K⁺- and Cl^--channels, through which the two ions leak through the cell membrane.

Intestinal and kidney tubule cells transport substrates, such as glucose and amino acids, in a substrate-Na⁺ cotransport in the luminal membrane, linked to the Na⁺-K⁺-pump of the basolateral membrane. This is called a secondary active transport of substrate. Such a transport is powered by an actively established gradient (ie, the Na⁺-gradient)

The many ion-transporting ATPases form classes or families showing amino acid sequence homology.

1e. Glucose transport proteins (GLUTs) and insulin receptors

A family of homologous carrier proteins that are coded by distinct genes mediates glucose-transport. The transport proteins (GLUTs) show a marked tissue-specificity, which reflects differing transport needs of various tissues. This is facilitated transport (Fig. 1-2).

Five human glucose-transporters are cloned and identified (GLUT 1-5). The GLUT 1 resides in placenta, brain, perineural sheaths, red cells, adipose and muscle tissues. GLUT 2 is found in the liver, pancreatic b-cells, proximal renal tubule cells, and the basolateral membranes of small intestinal cells. GLUT 3 is ubiquitously distributed, found predominantly in the brain and in lower concentrations in fat, kidney, liver and muscle tissues. GLUT 4 is confined to tissues with insulin-responsive glucose uptake (muscle, heart and fat stores). GLUT 5 is found in the luminal membrane of small intestinal cells, and also in brain, muscle and adipose tissues. Some of these transporters also allow fructose and galactose to pass.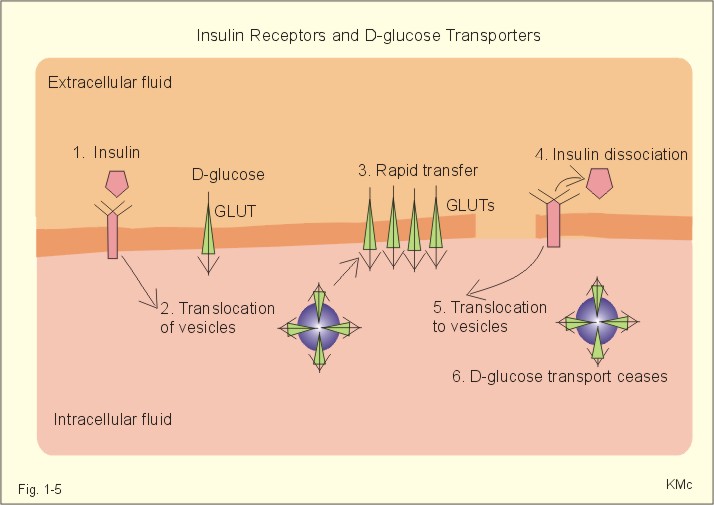

Fig. 1-5: Insulin, insulin receptors, with D-glucose transport proteins (GLUTs) and their translocation.

In adipocytes and muscle cells, glucose transport is profoundly influenced by insulin (Fig. 1-5).

1. As insulin binds to its large T-shaped insulin receptor, many intracellular vesicles are stimulated.
2. They contain a high number of membrane penetrating GLUTs, which translocate from the intracellular pool towards the cell membrane.
3. When these vesicles - rich in glucose transporters - fuse with the cell membrane, the number of glucose transporters increases substantially, thereby increasing D-glucose uptake up to ten times.
4. As the insulin-receptor complex dissociates, the GLUTs translocate again to the intracellular stores in the vesicles (Fig. 1-5).
5. The glucose transport ceases.

The insulin receptor is a glycoprotein found in the cell membranes. The T-shaped receptor protruding from the cell membrane contains 1370 amino acids forming two a- and two b-sub-units. The two a-subunits are entirely extracellular, whereas the two b-subunits span the membrane. Insulin binding on a-subunits stimulates a protein kinase on the intracellular part of the receptor to phosphorylate tyrosine residues on the b-subunit and on endogenous proteins. The exact molecular mechanism linking the receptor kinase activity to changes in cellular enzyme activity and transport processes remain uncertain; but it is shown that the kinase activity is essential for signal transduction.

2. Resting membrane potentials

A membrane potential difference is conventionally defined as the intracellular (j ⁱ) minus the extracellular (j ^o) electrical potential. The ion concentrations (activities) inside the cell and outside the cell are called Cⁱ and C^o, respectively.

When a microelectrode penetrates a membrane, it records a negative potential with respect to an external reference electrode caused by different permeability of anions and cations. This is the resting membrane potential (RMP values in Table 1-2). The resting membrane potential is an essential mechanism in storing and processing information in neurons and other cells.

Concentration gradients across cell membranes are present for several ions, whereby they diffuse from one location to another. The ion with the highest permeability and concentration gradient, such as the potassium ion, establishes a membrane potential. This potential enhances or inhibits the flux of other ions and the ultimate situation is an electroneutral flux.

The chloride ion diffuses extremely rapidly, but otherwise positive ions (cations) diffuse more rapidly than negative ions (anions) through a membrane. However, as an example the permeability for Na⁺ is low (0.2 nm *s^-1) compared to that of K⁺ (5-40 nm/s) in neurons.

The equilibrium potential for a certain diffusible ion across a membrane that has a concentration gradient over the membrane, is precisely that membrane potential difference, which opposes the flux due to the concentration gradient so that the net transport of the ion concerned is zero. The equilibrium potential is simply calculated by balancing the diffusion potential of the ion with the opposing electrical force. The electrical force working on the ion is proportional to the electromotive force of the field. As a consequence, the total driving force on the ion and its diffusion flux is zero. Nernst introduced this equilibrium potential shortly before year 1900. The Nernst equation for the equilibrium potential of Na⁺ across a selective permeable membrane at 310 K is found by insertion of the ion activities (concentrations) inside and outside the cell (Eq. 1-5).

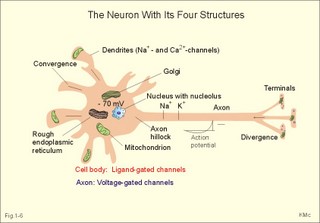
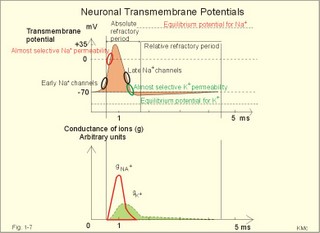
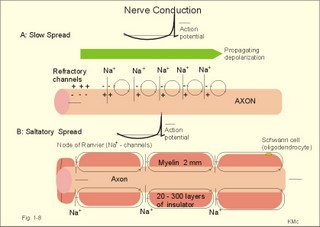
In skeletal muscle cells the resting membrane potential is -80 mV, and the equilibrium potential of Na⁺ is +60 mV. Hence, the electrical driving force is: (-80 - (+60)) = -140 mVolts. Accordingly, there is a net passive influx of Na⁺ into these cells down an electrochemical gradient (Table 1-2). The net influx is small because the resting Na⁺ penetration is almost exactly balanced by active extrusion.

The resting membrane potential (RMP) is calculated from the Millman equation (Eq. 1-8). The RMP is mainly a diffusion potential (see above).

Neurons typically have four structures: The cell body, dendrites, axon and axon terminals (Fig. 1-6). Dendrites are elaborate branching processes that arise from the cell body, and they are pathways for incoming signals from other neurons to the cell body. Integration of incoming signals occurs mainly in the axon hillock. This is the part of the cell body, which gives rise to an elongated tube called an axon, a fibre that can be up to 1.2 m long.

Fig. 1-6: The neuron with cell body, dendrites, axon and axon terminals.

Near its termination each axon divides into fine branches, each of which ends in an axon terminal (ie, synaptic button or Bolton terminal). The axon terminals contain mitochondria and synaptic vesicles filled with neurotransmitter. These presynaptic structures are the sites where electrical signals are converted into chemical messages for transmission to nearby neurons. Unipolar neurons only have a single major process extending from the cell body. Bipolar and multipolar neurons have two or more major processes arising from the cell body. Most neurons have only one axon, a few more than one and some neurons function without an axon. Their location, structure and functional properties (Table 3-1) classify neurons. Communication from an axon to a dendrite is called axodendritic, from a dendrite to another is termed dendro-dendritic, from a dendrite to an axon is called dendro-axonal, from a dendrite to the soma is called dendro-somatic, and between two axons is referred to as axo-axonal.

Neuronal membranes are composed of lipid bilayers stabilised by hydrophobic interactions, and thus function as barriers to free diffusion for water-soluble molecules. The ability of the neuronal membrane to control the movement and concentration of charged particles generates ion gradients with a charge difference across the membrane. The potential difference across the resting membrane is called the resting membrane potential (RMP).

Ion channels and gates are classified according to the gating stimulus to which they respond. Voltage-gated ion channels are located along the axon of a neuron and responsible for the action potential. These ion channels are sensitive to local anaesthetics. Voltage-gated Na⁺- K⁺- and Ca²⁺-channels contain membrane spanning helices – often with amino acid sequence homology. Action potentials in cardiac muscle cells have a plateau phase, where Ca²⁺ enters the cytosol via slow Ca²⁺-channels. This Ca²⁺-entry plays an important role in excitation-contraction coupling.

Ligand-gated ion channels are responsive to particular neurotransmitters. Ligand-gated ion channels open in response to substances such as acetylcholine. These channels are permeable to small cations (often unselectively: Na⁺- K⁺- NH₄⁺- and Ca²⁺). These channels are involved in generation of the postsynaptic potential and the endplate potential.

NaCl is found in high concentration outside the neurons, whereas [ K^+] is high inside the cell. These ion gradients maintain a constant leakage of NaCl into the cell, and a leakage of K⁺ out. The gradients are maintained by the Na⁺-K⁺-pump, which is thus controlling the resting membrane potential. Cl ^--ions distributes passively across most neuronal membranes and contributes little to the resting membrane potential, but they are important for the modulation of incoming signals. At rest, many K⁺ -channels are open and K⁺ moves down its concentration gradient out of the cell, whereby the inside becomes negatively charged (until it is difficult for K⁺ to leave the cell, and the K⁺-outflux slows down). The RMP approaches the equilibrium potential for K⁺.

3. The action potential

Neurons can carry electrical signals along their whole length without any loss of signal strength. This electrical signal is an all-or-none phenomenon, termed the action potential. The incoming signals to dendrites and cell bodies consist of small, graded changes (ie, small synaptic potentials) in the resting membrane potential caused by the actions of neurotransmitters and modulators. Synaptic potentials are spatially and temporally summated in the axon hillock of the cell body. The synaptic potential is graded according to the stimulus and shows decrement conduction in that its size decreases with increasing distance (wave length several mm). The local synaptic potential cannot in itself initiate an action potential. When the strength of the summated synaptic potentials is sufficient to reduce the resting membrane potential at the axon hillock below the threshold it opens Na⁺ -channels. These Na⁺ -channels are voltage-gated, because the change in voltage opens or closes a gate over each pore. The Na⁺ -channels is usually closed at conditions with a normal resting membrane potential. When the Na⁺ -channels open and allow Na⁺ to flow into the cell down its concentration gradient, the influx itself depolarizes the neuron further, whereby more voltage-gated Na⁺ -channels open. A propagating action potential (approaches the equilibrium potential for Na⁺) in the axon is generated with a positive voltage overshoot simultaneously with the peak membrane conductance to Na⁺ (g_Na⁺ in Fig. 1-7). This is followed by the repolarisation phase (conductance for Na⁺ goes down and up for K⁺), when the potential returns toward the resting membrane potential. The potential may overshoot the resting value, causing a transient hyperpolarization known as the hyperpolarising afterpotential (Fig. 1-7) close to the equilibrium potential for K⁺.

Sustained depolarization inactivates the voltage-gated Na⁺ -channels, and shuts off the Na⁺ -influx. Opening of voltage-gated K⁺ -channels allows an increased outflux of K⁺ to counterbalance the influx of Na⁺. The membrane conductance to K⁺ increases slowly, and reaches a peak in the repolarization phase (g_K⁺ in Fig. 1-7). This K⁺ -outflux causes the neuronal membrane potential to return to its normal resting value, when the Na⁺ -channel is inactivated. The signal conduction is unidirectional, because newly opened Na⁺ -channels become refractory for a time, when they are inactivated. As these areas are blocked for further depolarization for a time, the depolarization can proceed only in the forward direction towards resting Na⁺ -channels.

Fig. 1-7: Transmembrane potentials and Na⁺-K⁺- conductance (flux) in a neuron.

The action potential is an all-or-none electrical signal, which appears as a positive wave when recording internally. The action potential is conducted with the same shape and size along the whole length of a muscle cell or a nerve fibre.

The refractory periods

During the early part of the action potential the cell membrane is completely refractory. A new stimulus, regardless of its size, cannot evoke an action potential. Almost all Na⁺-channels are inactivated, and will not reopen until the cell membrane is repolarized. This is the absolute refractory period covering most of the peak and lasting until well into the repolarizing phase (ARP in Fig. 1-7).

During the hyperpolarizing afterpotential, a suprathreshold stimulus is able to trigger a new AP, albeit of smaller amplitude than the first action potential. This period is called the relative refractory period (RRP in Fig. 1-7). The cell membrane is relatively refractory, because some Na⁺-channels are voltage-inactivated and at the same time K⁺-conductance is increased.

Nerve conduction

The lipophilic core of the cell membrane is an electrical insulator, but the salt solutions of the cytoplasm and the extracellular fluid act as conductors of electrical current. Opening of many voltage-gated Na⁺-channels, whereby the Na⁺-conductance is increased about 104-fold, so the membrane is instantly depolarised, causes the action potential. The action potential essentially spread by alterations of the voltage-gated Na⁺-channels.

Depolarization spreads along the membrane of excitable cells by local currents flowing to the adjacent segments of the membrane. This is shown in Fig. 1-8A. The phenomenon is called the local response or electrotonic conduction. The depolarization decreases mono-exponentially from the excitation site. Na⁺-channels will be recruited in all areas of the membrane, where the threshold potential is exceeded. The Na⁺-channels behind the peak of the action potential are refractory. This explains why an action potential travels in both directions, when it is evoked in the middle of a nerve.

Fig. 1-8: Spread of the action potential along an unmyelinated (A) and a myelinated (B) axon. The refractory channels prevent the action potential from proceeding in more than one direction. The action potential (wavelength in cm) essentially jumps from node to node or over several nodes facilitating high-speed conduction.

The myelin sheath consists of 20-300 layers of insulator substance produced by Schwann cells wrapping round the axon. The nodes of Ranvier are the lateral spaces (1 mm wide) between adjacent Schwann cells, which stretch 1-2 mm.

The effects of this arrangement are as follows:

Very little current is lost through the electrical insulation of the myelin sheath. Thus, the electrotonic conduction is rapid with only a small decrement in amplitude. The electrotonic conduction is virtually instantaneous. Because of the insulation the depolarization can spreadmuch faster.

Saltatory or leaping conduction occurs, because the action potential is generated only at the nodes (Fig. 1-8). The cell membrane below the myelin sheaths has hardly any Na⁺- channels and is therefore inexcitable. Saltatory conduction is up to 50 times faster than the conduction through the fastest unmyelinated axons. The action potential can also jump over a number of nodes to that farthest away, because the action potential wavelength is several m.

The Na⁺-channels there are activated by the electrotonic conduction.

Since the ionic currents are restricted to the nodes of Ranvier in the myelinated axons, this minimises disturbances in the Na⁺- and K⁺-gradients, that are restored by an active process in which the Na⁺-K⁺-pump, driven by ATP, pumps Na⁺ out and K⁺ into the cell. The main energy cost is to restore the Na⁺- K⁺- balance.

Myelination of the nerve fibre thus reduces energy cost of maintaining the resting membrane potential following an action potential.

Typical values for normal ion concentrations (intracellularly and extracellularly) are given in Table 1-3.

The total calcium concentration in plasma is 2.2 – 2.7 mM, but only 45% is ionized (Chapter 30).

Pathophysiology

1. Hyponatraemia is defined as a plasma-[ Na^+] below 135 mM. This is a common condition caused by a high water intake (water intoxication), reduced water excretion in kidney disease, salt loss or other causes described in Chapter 24.

Hyponatraemia must be distinguished from the rare condition pseudo-hyponatraemia. Spuriously low [ Na^+] are measured in plasma (Na⁺ is predominantly confined to the water phase), simply because its concentration is expressed per l of plasma. Normally, 93% of plasma is water, and the non-water fraction is 7% (mainly proteins). In cases with too much lipid, protein, glucose, urea, or alcohol in the blood plasma (ie, hyperlipidaemia, hyperproteinaemia, hyperglucosaemia, uraemia, alcoholaemia etc), the normal [ Na^+] is reduced by dilution with the increased non-water fraction. Thus, the calculated plasma-osmolality (Eq. 1-7) is less than the freeze-point-measured osmolality. This discrepancy is called the osmolality-gap.

There is no need for treatment with salt-solutions in such spurious conditions. Pseudo-hyponatraemia also occurs, when a blood sample is taken from an arm vein, where a glucose solution is infused. The plasma-[ Na^+] obtained from such a blood sample is low.

2. Overbreathing is also called hyperventilation. Overbreathing is frequently caused by panic attacks (ie, hyperventilation tetany). The high ventilation washes out too much carbon dioxide (CO₂)/carbonic acid, whereby the CO₂ tension of the arterial blood decreases simultaneously with an increase in its pH. This is an alkalosis (arterial pH above 7.45). Alkalosis dissociates proteins by mass action and form Ca²⁺-proteinate (Fig. 17-9). The falling extracellular concentration of free Ca²⁺-ions reduces the threshold and opens Na⁺-channels in neurons, muscle cells and myocardium. The resulting reduction in membrane potential increases the excitability of the tissues, which causes continuous muscular contractions (ie, tetanic cramps).

Equations

• Uniformly distributed substances in diluted solutions behave like gas molecules at atmospheric pressure (atm). The osmotic pressure can be expressed as:

Eq. 1-1: P_osmot = C * R*T,

which is the equivalent of the ideal gas equation (P = n/ V* R*T). C is the concentration of dissolved solute. R is the gas constant (= 0.082 l atm mol^-1 K^-1).

• Fick's first law of diffusion deals with the diffusive flux per m² :

Eq. 1-2: J^dif = -D* dC/dx.

The dimension of D is found by dimension analysis of the equation for J^dif:

Accordingly, D has the dimension: m² s^-1. D is small, when the molecules are large and when the surrounding medium is viscous. The permeability coefficient (ie, permeability) for a membrane is the flux (mol m^-2 s^-1) divided by the concentration (mol m^-3) for a given substance and has the unit m s^-1.

Eq. 1-3: (dx)² = 2 * D * t.

Eq. 1-4: p = T× R× f × N/V or p = T× R× DC

where R is the ideal gas constant (0.082 l × atm ×mol^-1 × K^-1 or 8.31 J (K mole)^-1 ), and DC is the concentration gradient. This is the law for ideal or extremely dilute solutions.

Eq. 1-5: j ⁱ - j ^o = (R T/z F) ln(C^o_Na⁺/Cⁱ_Na⁺) Volts (V)

V_EqNa⁺ = 61.5 log (C^o_Na⁺/Cⁱ_Na⁺) mV.

In the equation above R is the ideal gas constant (8.31 J (K× mole)^-1), T is the absolute temperature, z is valence of the ion with sign (z= +1), and F is the Faraday constant (96 500 coulombs per equivalent). The activity coefficient for sodium is 0.75 and used to convert concentration to activity.

Eq. 1-6: N = N_o * e^{-k t}.

where k is a constant characteristic of each nucleide, called the disintegration constant.

Eq. 1-7: Plasma-osmolality = (2* [ Na^+] ) + [ glucose] + [ urea]

Normally, the plasma-[ Na^+] is 140 mmol in 1 litre of water, and both plasma-[ glucose] and plasma-[ urea] are around 5 mmol per l of water. The plasma-osmolality is given in mOsmol per kg of water. One l of water is approx. equal to 1 kg of water.

The Millman equation. A convenient version to calculate the resting membrane potential (RMP) at body temperature is:

Eq. 1-8: RMP = (g_K⁺×Eq_K⁺ + g_Na⁺×Eq_Na⁺ + g_Cl-×Eq_Cl-)/(g_K⁺ + g_Na⁺ + g_Cl-)

This equation shows that the RMP is determined by the conductance (g) of the membrane to K⁺, Na⁺ and Cl^-, and by their equilibrium potentials.

Self-assessment

Multiple Choice Questions

I. Each of the following five statements have False/True options:

1. Positive ions (cations) diffuse more rapidly through a membrane than negative ions (anions).

2. The Na⁺-K⁺ -pump located in the cell membrane, is responsible for maintaining the high intracellular [K⁺] and the low intracellular [Na⁺].

3. The permeability for Na⁺ in cell membranes is high compared to that of K⁺ and Cl^-.

4. In skeletal muscle cells the resting membrane potential is -80 mV, and the equilibrium potential of Na⁺ is +60 mV.

A membrane potential difference is conventionally defined as the extracellular minus the intracellular electrical potential.

II. Each of the following five statements have False/True options:

1. The local, subthreshold response is graded according to the stimulus.
2. Accommodation is a progressive decrease in firing frequency despite maintained depolarization.
3. Voltage inactivation of Na⁺-channels is involved in the accommodation and in the refractory periods.
4. During the early part of the action potential the cell membrane is relatively refractory.

Voltage-gated Na⁺-, K⁺- and Ca²⁺ -channels are comprised of subunits with membrane spanning domains.

1. Saltatory conduction is up to 50 times faster than the conduction through the fastest unmyelinated axons.
2. Saltatory conduction occurs because the cell membrane beneath the myelin sheaths has a high density of Na⁺-channels.
3. At standard temperature, pressure, dry (STPD) the volume occupied by 1 mol of any ideal gas is 22.4 l.
4. Elimination with decreasing rate is exponential.

Facilitated diffusion shows saturation kinetics, and takes place through transport proteins not linked to the metabolic energy processes.

1. Osmolarity is the number of osmotically active particles in each l of solution.

2. Facilitated diffusion does not show saturation kinetics but moves solutes up-hill.

A family of homologous carrier proteins that are coded by distinct genes mediates facilitated diffusion.

3. Glucose-transport. The transport proteins (GLUTs)   show a marked tissue-specificity which reflects differing transport needs of various tissues.
4. The relation between the potential difference measured with an ion-selective electrode and the activity is given by the Nernst equation.
5. The Donnan effect is the extra colloid osmotic pressure of protein solutions caused by uneven distribution of small, diffusible cations and anions.

Try to solve the problems before looking up the answers.  

Highlights

• In cases with too much lipid, protein, glucose, urea, or alcohol in the blood plasma (ie hyperlipidaemia, hyperproteinaemia, hyperglucosaemia, uraemia, and alcoholaemia) etc, the normal plasma-[ Na^+] is reduced by dilution with the increased non-water fraction.
• Overbreathing is caused by panic attacks. The high ventilation washes out the carbon dioxide (CO₂)/carbonic acid, whereby the CO₂ tension of the arterial blood decreases simultaneously with an increase in its pH. This is an alkalosis. Alkalosis dissociates proteins and form Ca²⁺-proteinate. The falling extracellular concentration of free Ca²⁺-ions opens Na⁺-channels in neurons, muscle cells and myocardium. The resulting reduction in membrane potential increases the excitability of the tissues, which causes continuous muscular contractions (ie, tetanic cramps).

Further Reading

Bruce Alberts, Alexander Johnson, Julian Lewis, Martin Raff, Keith Roberts, Peter Walter,Molecular Biology of the Cell, Fifth Edition.Garland SG, 2007.

Apps DK, BB Cohen, and CM Steel. "Biochemistry." Bailliere Tindall, London, 1994

Return to content

Return to chapter 1